There are 18 symbols available in our matchstick tasks: 10 numerals, 4 operators and 4 comparators. They are each built with a set of matchsticks (from 1 to 7) in a specific commonly recognized pattern.
For consistency all matchsticks are aligned with matchstick's head directing upwards (primary) and left (secondary).
Numerals can easily be represented in a seven-segment display framework, which is commonly used in electronic devices that display numerical information. It was invented in 1970 as a spin-off of the 8-segment display and reached its peak with the advent of LEDs in the 1970s. But although it is not commonly used since the widespread use of dot-matrix LCDs, it is still widely recognizable.
|
|
|
Original source: https://en.wikipedia.org/wiki/Seven-segment_display
Four basic binary operations can easily be built with matchsticks. Those operations include addition ( + ), subtraction ( - ), multiplication ( * ) and division ( / ), and they suffice for our experiment. Other, more complex operations can also be represented with matchsticks, but arguably harder, and as they are not really required for the scope of our experiment, we will set them aside.
Addition can be represented by a plus ( + ) symbol, made up of two matchsticks, one laid horizontally and one perpendicular to it crossing it in the middle.
Subtraction can be represented by a minus ( - ) symbol, made up of only a single matchstick, laid horizontally.
Multiplication can be represented by a multiplication sign X, which can be made up of matchsticks, unlike the dot multiplication symbol ( ⋅ ). It can be made like a plus sign tilted by 45 degrees.
Division sign can be represented by a forward-slash ( / ), which can be made up of a single matchstick, much like the minus sign, but tilted by 45 degrees counter-clockwise.
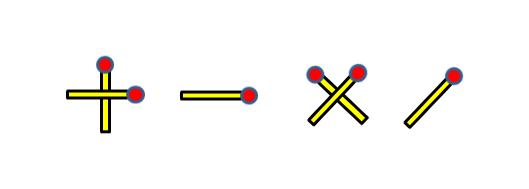
Four basic matchstick operations in following order: addition, subtraction, multiplication and division,
A symbol for equality ( = ) can be achieved by putting two matchstick horizontally in parallel.
The symbol for in-equality ( ≠ ) can be created by adding a diagonally facing matchstick (much like division symbol) on top of the equality sign.
Also, symbols for non-equality ( < and > ) can be added to provide an increased variety of options to solve provided equations. They can be created by adding an inversed division symbol above ( > ) or below ( < ) another division symbol. There is also option to add non in-equality signs: ≤, ≥, but this seems way to complicated to be feasible for actual use. However, it is completely possible to implement those options.
Suggestion
A list of all allowed symbols should be given to the subject beforehand in order to prevent later misunderstandings.
How can a single symbol be changed by an act of adding or removing a matchstick?
Numerals follow a very different matchstick frame (7-segment display) than operations and equality signs. Thus, in normal circumstances, by actions of adding or removal of matchsticks numeral symbols cannot become operator or equality symbol and vice-versa. There are situations that this rule can be broken and the symbolical representation retained, but we should not allow that at all to simplify the experiment.
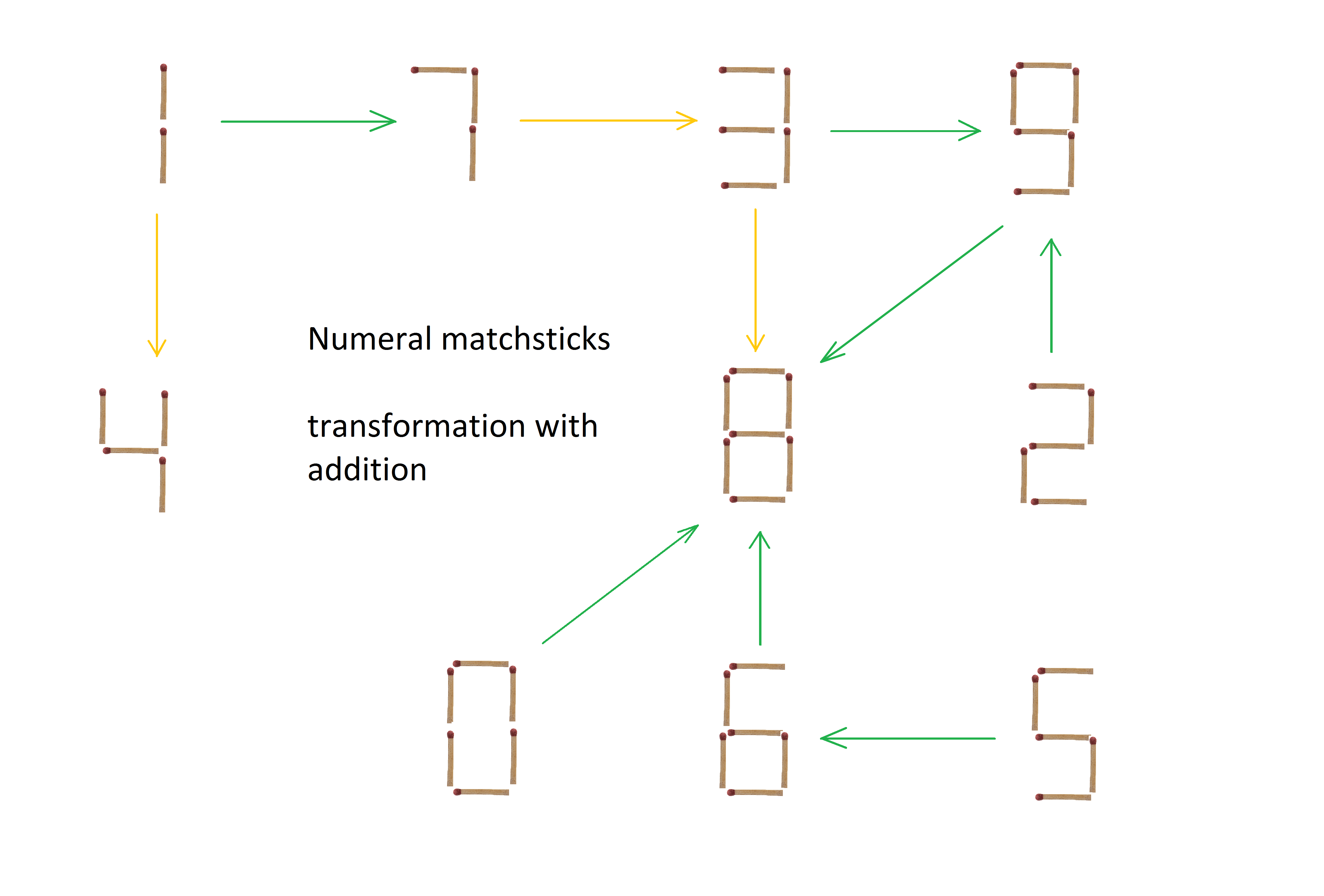
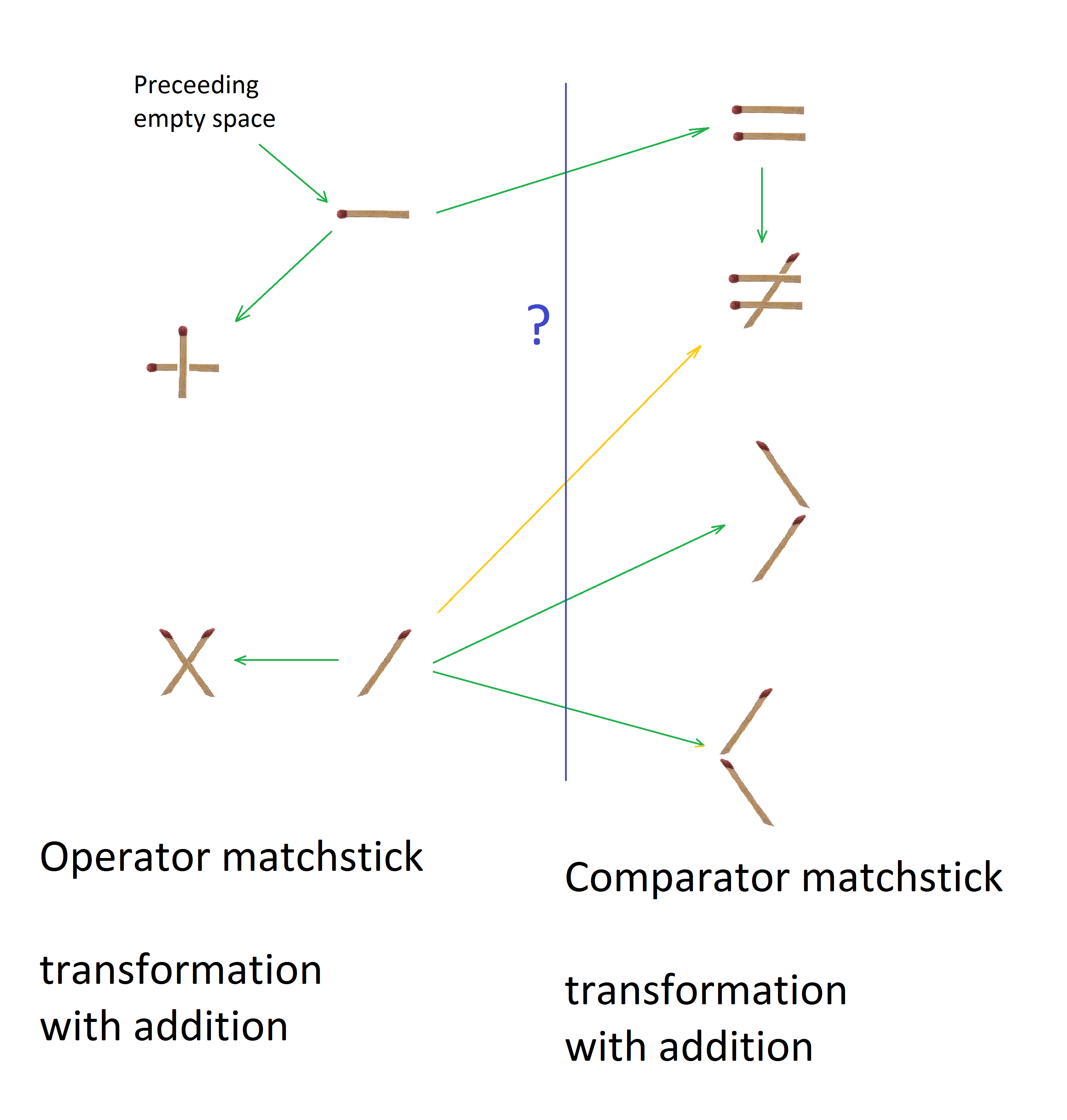
The two pictures above are a simple visual representation of symbol changes. Green arrows mark addition of a single matchstick and yellow matchstick addition of 2 matchstick(not all available yellow lines are drawn). Arrows can be also thought in reverse to show what a removal of matchsticks can produce. The function of these pictures is purely illustrative, to show how many simple changes are available to transform symbols.
The table below contains all possible results for actions -1, +1 and a move of one matchstick.
| Original | Added and removed matchsticks | |||
| +1 |
-1 |
+1 -1 | ||
| 0 |
8 |
0, 6, 9 |
||
| 1 |
7 |
1 |
||
| 2 |
|
2, 3 |
||
| 3 |
9 |
2, 3, 5 |
||
| 4 |
4 |
|||
| 5 |
6, 9 |
3, 5 |
||
| 6 |
8 |
5 |
0, 9 |
|
| 7 |
1 |
|||
| 8 |
0 |
|||
| 9 |
8 |
3, 5 |
0, 6 |
|
| + |
- |
|||
| - |
+, = |
/ |
||
| x |
/ |
|||
| / |
x |
- |
||
| = |
≠ |
- |
||
| ≠ |
= |
|
||
For higher actions this search becomes more difficult and not feasible to be completed by hand. Furthermore, combinations of these element changes have to be calculated and such equations created and tested for correctness. This is practically impossible to do by hand. Therefore, a program will be written to test all the following: single symbol changes, full equation changes when actions are applied and equation correctness, to ensure the task is solved. Preferably all options will be tested (in brute force strategy), but at a bare minimum sets of equations will be created, which will be further used as tasks for specified experimental groups.
