
Unofficial data and image sources:
http://www.business2community.com/tech-gadgets/top-20-popular-programming-languages-2017-01791470#JTtd1CJacuBLYGh0.97
In accordance with discussion on meeting #01, some simple programming tasks with multiple perspectives should be found.
As discussed on meeting #02, proper experimental tasks should be created from the these tasks.
On this page, simple programming tasks that NG has found are presented.
Arrays and Lists
The structures have very common usage in every-day programming. However, I'm very reluctant as to say they have different mental representations. My own mental representation of one or the other does not differ significantly. They are one of the most basic structures in programming.
There are well known clear features and advantages for each of them.
Trees
Tree structures expand a little bit on arrays (direct children access) and lists (children is list form), but offer significantly different mental representations. However, these structures are a bit more complex, when compared to basic arrays and lists.
There are well known clear features and advantages for each of them.
In complexity, these tasks are comparable to Simon's task of Size and Distance problem.
Representation and Transfer in Problem Solving.pdf
However, the structures DO DIFFER a little in functionality, and not only in mental representations as in Simon's task. I am unsure if there is a possibility to have piece of code with two different mental representations. Judging from Python's inability to distinguish lists and arrays, there could be something on to it: Programmers using Python's structure can have array or list representation - or there could be just a totally different representation for that.
Programming tasks heavily depend on the programming languages they are being solved with. Each programming language provides unique tool-set of functions, methods and mechanisms that are to be used when solving the task. And in this way, the tools used can influence the final solution and the problem-solving process significantly. But the differences don't stop there. Apart from providing different sets of problem-solving tools, programming languages can differ in the mental representation and problem understanding as well. Depending on how they frame (what is the mental model behind them) the presented problem, programming languages are grouped in programming paradigms. More information on these can be found in my previous research, where I tried to see how much these programming paradigms influence mental models of Tower of Hanoi problem.
Because of said importance of programming language selected, it is important to be aware of their influence on problem-solving processes. I propose we chose a single programming language for all of our tests to nullify the effect of different programming languages (and subsequently, different programming paradigms) on our research. A single selected programming language would provide us with a single baseline mental model, which is encapsulated by programming-language's programming paradigm. This model, however, is not strict and should be understood more as a mental guideline - a lot of different mental representations and models of a specific problem can be made with little or none deviation from the programming-paradigm's mental model. This offers us enough of space to test subtle, but significant differences with mental models.
In case this has not been well understood: Programming paradigm of programming language Java is known as Object-oriented paradigm. Its default mental model is to represent problem elements as identifiable and comparable objects with specific set of properties, which defines them. This may seem strict and narrow minded, but solver is free to determine what those objects mean to him and how he will define and use them in solving his problem.
In the following few lines, I will explain why programming language Java (v1.8) is the one we should focus on as our primary favorite. In no way I am saying that this programming language is the best. It is just good enough and I believe choosing it, can significantly improve our research than choosing any other programming language.
Important: All following tasks will be constructed to be solved in this language!
Why I chose Java:

Unofficial data and image sources:
http://www.business2community.com/tech-gadgets/top-20-popular-programming-languages-2017-01791470#JTtd1CJacuBLYGh0.97
The tasks, described below, are to be understood in the context of programming language Java.
Similarity between arrays and lists is great. Both are used to hold linearly sorted data, but each on its own way.
| Array |
List |
|
|
An array is a container object that holds a fixed number of values of a single type. The length of an array is established when the array is created. After creation, its length is fixed. Each item in an array is called an element, and each element is accessed by its numerical index. As shown in the following illustration, numbering begins with 0. The 9th element, for example, would therefore be accessed at index 8.
(Source: https://docs.oracle.com/javase/tutorial/java/nutsandbolts/arrays.html)
|
List is an ordered collection (also known as a sequence). The user of this structure has precise control over where in the list each element is inserted regarding the neighbors. The user can access elements by their integer index (position in the list), and search for elements in the list.
(Image source: http://4.bp.blogspot.com/-ZQub4l3oliM/UfKzmX88ofI/AAAAAAAACQw/uIdj4ZF1Y4Y/)
|
|
|
Usage example (Java):
// initialization (size 5) int[] arrayExample = new int[5]; // adding elements (on 4th place) arrayExample[3] = 6; // retrieving elements int n = arrayExample[3];
|
Usage example (Java):
// initialization List listExample = new List<int>(); // adding elements (to the end of list) listExample.add(6); // retrieving elements (from the 4th place) listExample.get(3); |
|
| The beauty of an array is in its fixed size and the ability to access any stored value directly. However, from here also comes their greatest limitation: inability to change. If a size extension is needed, a new, bigger array must be created and data copied from the old one. | The list is a very flexible structure, as it can hold arbitrary number of elements in a sequence. Here is no size limitation, however none of the elements can be missing and elements are not always in the place they were put in. As list constantly fixes its structure, the value indices (position numbers) may get shifted, due to elements being added to / removed from the list. Additionally the size can be unknown. | |
|
Real-world analogy: Mailboxes
Mailboxes in a block of flats can be used as a great analogy to describe the ability of array structure. Mailboxes are built together and there is always a fixed number of mailboxes in a certain building - the number corresponds to the number of apartments in the building, there can be no more and no less of them. The mailboxes are also numbered in a sequence, where each mailbox number corresponds to a unique apartment number. By knowing the mailbox number, one can easily identify the correct mailbox. Let us presume we want to hide a set of yellow ping-pong balls and one blue ball in those mailboxes. + To know in which mailbox the blue ball is, one must just remember the mailbox number. This way the blue ball can be accessed directly. - To put a blue ball into the specific-number mailbox, which currently contains a yellow ball, one must first take the yellow ball out of the mailbox. - We can only have as many balls as there are mailboxes. If there are more balls, we cannot put them anywhere and it is also not a good practice to have too few balls and thus empty mailboxes (because empty mailboxes do cost space, which could be used better). If one finds himself with too many balls, he must usually abandon the current building and find another one with enough mailboxes to fit all the balls in. |
Real-world analogy: Train wagons
Train wagons can be used as a great analogy to describe the list structure. Wagons are linked to one another in a way, that each wagon provides a hook at its end, on which another wagon can be attached. This way the train size is practically unlimited, as more wagons can be attached, if needed. Wagons can be added or removed fairly easy, as all it takes is just to attach them in the desired place in the sequence. Because of this feature, wagons are not numbered, as their position in the line can easily change. Let us presume we want to hide a set of yellow ping-pong balls and one blue ball in those mailboxes. + Train can support any number of balls, as wagons can be added or removed as necessary. - We need to keep track of which wagon the blue ball is in. As the wagons are added or removed, their position in the sequence changes. We must keep track of it or each time check all of the wagons to find the one with the blue ball. - Additionally, to get to some wagon, one ALWAYS starts from the engine (beginning of the train) and makes his way along the wagons, having to go through all preceding ones to get to the desired one. Wagons are not accessible by their position number! To get to the next wagon, one just needs to check the hook on the current wagon and what is attached to it. If there are no wagons attached, that means one has reached the end of the train. |
Another issue that should be noted in popular programming languages (like C and Java) is that these two structures have been developed in a way that their real implementation is hidden from the user. They both have added functionality that user might find extremely helpful. If an element is added as an extra element to the array, the program can silently create a bigger array and copy the elements into the new one and in this way "expand the array" without user's knowledge. Similarly for the list, functions that return its current size and an element in the certain (numbered) position are a common thing. User is often not required to use those additional functions, but they are always at his disposal and available to him.
Programming language Python has gone so far that arrays and lists have been merged into a single structure and are thus indistinguishable from one another.
These additional functions are far from optimal! However, in the world of programming they present very little practical overhead. Creating additional array for 100 000 elements and moving all of those elements to the new array, might prolong a simple program by more than 1000%, but in real time that will only roughly take additional millisecond. For a lot of programs, this is considered a good-enough practice.
Arrays and lists are used for the same purpose - having elements in an order and interacting with them - and they can always interchange regardless of the task presented. If one can solve the task, so can the other. By the way they are implemented in a specific language, their interchangeability can slightly differ, but with a few mild extensions and workarounds, they can both be used to solve the same task. Having common usefulness, they sure differ in the mental models and representations they enforce. One must consider and imagine the elements' container in a different way, which is often accompanied with a different mental image of those elements' positions and relations to one another.
We can exploit this representational, but not usage, differences between arrays and lists for the purposes of our project. We want to know how one can represent these structures internally and why does he chose to do so, why does he use one and not the other. Gaining this knowledge, we will come a step closer to understanding how and why certain mental representations are created/used and how these representations effect the problem solving process and the final solution.
A task can be created regarding the sequence of the elements. For example, a simple sorting task is complex enough to encapsulate all of the mayor points that we need to research: Subject is given the numbers and is asked to return them sorted in an order from the smallest to the largest (for example; we can also use other orderings to observe any differences). Additionally, the subject is given the programming environment (a computer with programming tools supported, perhaps an IDE as well) and instructed not to use any of imported tools. This way, he must create all of the tools, he decides to use, himself. Tool creation is in this way a very important part of solving this task. The whole task itself is not considered difficult (even the tool creation part) and can be done in a couple of minutes.
!TODO Explain this task (and why it was chosen)
But, because of limitations, described in the following section, we cannot use this task.
Unfortunately, due to allocation restrictions, Java does not allow the creation of a personal array. Only the one that is defined in the programming language itself can be used. This issue disables the gist of our task, that users would create their own arrays to solve the task. There are a couple of ways to try and fix this issue, but none of them are viable.
But fortunately another tasks exists, which we can use! Programmable trees.
The tree is a great tool to use when data has to be hierarchically sorted in a parent-child or master-slave relationship. This is a way where each element has exactly one superior/parent (except root element) and can have any whole number of children. When put into a tree structure, each element is assigned a node (much like a place in an array or list), which holds the data about its relationships with other nodes in the tree.
Root node is the top node in the tree and the only node which does not have a parent.
Leaf node is the node without any children. Null reference marks the point where a child could be (if there would be one).
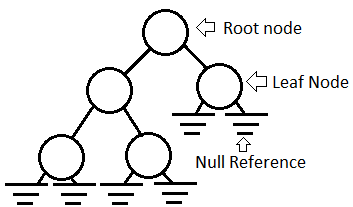
(Image source: http://www.c-sharpcorner.com/UploadFile/4a950c/5079/Images/1.gif)
Binary tree is a special kind of tree, in which each node can have at most 2 children. This is the only added limitation and difference from other trees.
Implementation of trees can significantly vary, as a common tool is currently not agreed upon by programming community.
Best practice is for one to create a tree structure when needed and according to current needs.
If one is exposed to the idea of a programmable tree for the first time, it can be (as all programming 'stuff') quite confusing. So, let us start from the beginning. The idea of programmable trees as well as their name originates from physical trees and their branches - especially relations between them. Part of tree that is above ground consists of trunk (which we will consider as just another big branch), branches and leafs. From the roots grows the first branch (or trunk), from which a couple of other branches spawn. Each of these branches later spawns a new set of branches, which in turns spawns other new branches, and so on. Sooner or later this trend ends in a branch that has no further branches. Continuing from above analogy, a branch with no further branches is called a leaf.
See image for better understanding. Image source: http://dragonlordwarlock.com/blog/wp-content/uploads/2012/10/tree.png

In the image above is depicted a binary tree (each branch spawns only 2 new branches). A branch on a normal tree can however have an arbitrary number of branches (positive number, and including zero).
To transfer idea, presented above, into the programming world, we must make some term adjustments. The term branch gets replaced with the term node, the term trunk with the term root node (because it does not originate from another branch, but instead from roots. Next, the term leaf with the term leaf node (bottom line: no nodes continue from it). And lastly the relationship between branches/nodes B, C and D, originating from the branch/node A, is referred to as: B, C and D are children of A and in turn A is the parent of B, C and D. That is all there is to know about terminology.
To use programmable trees in practice one must first find a good use for them. A good example is a family tree.

Let us take just the male side of this family for better explanation. We are not interested in their ancestors, so let us presume the grandfather is at the source/root of this family tree. The grandfather (root node) has 2 child nodes, which are brothers between themselves and grandfather is their parent node. Each of them has three child nodes of his own. And those nodes are yet too young to have children of their own, they are considered leaf nodes.
The same example stands for the employees in a company: CEO has 2 managers and each of them has control over 3 employees.
There are endless examples. The main point is that they all have this in common: Elements are hierarchically set and each element has one parent (except root) and 0 to n number of children. Every problem that fits this description can make use of programmable trees.
Often trees are turned upside down in graphical presentations, in order to emphasize the root element and hierarchical structure. Both representations are valid and they represent the same structure - one can use either of them. We are going to use root-top presentations from now on for all representative purposes, solely because I prefer that representation.
| Children direct |
Children in list | ||
|
Tree children can be referenced directly. Each node has a fixed number of children that can be accessed directly via variable name or a number.
|
Tree children can be accessed in order from first to last. To access the third child of the node A, one must first access the first child from the node A, then access his brother (second child) and from there the second-one's brother - the third child.
|
||
|
Sample minimal code for binary tree (Java object):
class Node { // the actual value node contains Object nodeValue; // link to left child Node leftChild; // link to right child Node rightChild; }
|
Sample code for n-children tree (Java object):
class Node { // the actual value Object nodeValue; // array of children Node[n] children; } |
Sample code for tree (Java object):
class Node { // the actual value node contains Object nodeValue; // link to the first child Node firstChild; // link to the right/next brother Node next; }
|
|
|
As shown on this image and accompanying code, each node has two or n children that are accessed directly via variables or child_number. The number of children cannot be changed. Children are forced to be listed in a sequential order. Each child can be referenced by his stance, comparing to other children. Eg. left child or child no. 3. To be used when number of children is fixed and/or children have to be accessed directly.
A list of children can be used instead of an array. As discussed in arrays & lists section, this approach provides different (not necessarily better) features.
class Node { Object nodeValue; List<Node> children; }
This approach however does not fit into 'children in list' section on the right. Mainly because children are contained in the list and do not for the list itself (as they do on the right). |
As shown on this image and accompanying code, each node has a reference to its first child (or null, if it has no children) and a reference to its next brother (or null, if it is the last child). Each node can have arbitrary number of children. Children can be easily added and removed, but harder to access (one must go through it all previous brothers).
To be used when number of children is unknown and/or children are often iterated over. |
||
|
Real world representation: See family tree above.
Children are referenced from the view of their parent. |
Real world representation:
In the family tree situation, the children would be referenced from the view of their brothers; get_the_first_child, get_his_brother, get_the_second_brother_down_the_line, and so on.
A better fit would be perhaps a hallway model. Each hallway has doors on the side, which are listed in an order. And behind each door is another hallway with doors, and so on. Consider the first hallway the root node and doors on the side as its children. One can only reach the desired door by passing past previous doors in order they are set. So, in order to get to the 3rd door, one must first pass the first door, then the second door and lastly arrive to the third door. |
||
| It is difficult to provide examples for these cases, as both models are perfectly able to implement all of them. The change is only in the way the children are mentally represented; as descendants of their parent or as brothers standing in a line. | |||
Those are just two main ways of defining a tree structure. The left (direct) one is probably more common, but both of them can be found in practical implementations. There is very little representational differences, comparing to arrays' & lists' differences. These structures should be understood as kind-of upgrades upon arrays and lists to create a whole new structure. And in this way the differences between the initial structures (arrays & lists) are blurred by new common tree features.
Going back to previous problems on arrays & lists task. Arrays are inherent tools to Java environment - this means that since creating own arrays has been disabled, the current tool was integrated into Java language itself. In this way we cannot get around the usage of built-in array structure. If we prevent subjects to use (imported) list tools, this may seem like a great bias towards arrays, however it is not definitely so.
Implementing lists requires subject to create a structure mode that contains two things: (1) an element value and (2) a link to the next element in the list. By creating tree nodes we already provided a node entity that holds element value. From here on to implement list structure of children is a very minor task: it requires 2 additional lines of code, compared to 1 additional line when using arrays (or 2 lines when using variables). From the code point of view, both 'direct children' and 'children in list' methods are of the same complexity (judging from amount of code).
My speculations: From cognitive perspective, however, it seems that 'children in list' method is less available. But, I cannot confirm this without an experiment. I do suspect the results could be similar to Simon's experiments, where he concluded the size representation to be more available.
These tree structures are the most basic ones. A simpler form cannot exist, as here are used only the minimum requirements a tree structure needs. If there exists another minimal variation is unknown. Of course, variations of both exist, usually with added structures that bring positive aspects of both of above-presented structures into one more complex tree structure.
Again, the creation of the tool is the main part of the experimental task. As discussed above, both models have similar implementation complexity, but different mental representations and practical features (advantages and disadvantages). The only requirement is to prevent the use of imported List tools (and basically ANY additional imports) as that would mess up the separation that was made above: 'direct children' and 'children in lists'. This issue can be solved just by preventing all of the imports.
The task has to have a hierarchical structure; either family tree or business employee model or some other form.
!TODO: I will need a couple of days to come up with a practical hierarchical model, that should be least biased on one or the other implementation. We can always test multiple of those, but I am afraid that after the initial test, subjects may stick to the one model they used before. -> This can be tested in regards to transfer.
!TODO: Create a experimental task system.
Features of lists and arrays remain in these trees. So we can still "fuck with subjects" in a way that we require them to expand their initial solution in a way that their solution is not designed for; In 'children direct' we can add new/unexpected children and in the 'children in list' we can require children to be found by their position in the list.
Continuing upon the idea of sorting numbers with lists and arrays, a similar structure appears in the tree form as well: Binary search tree. These structures contain sorted set of elements (for example: numbers) in a binary tree form where for each given element / node the following is true: the left child and all of his descendants are strictly smaller then the current element and the right child and all of his descendants are strictly bigger then the current element.
This means that elements cannot be duplicated - it is a set of elements.
And all element searches (as well as adding and deleting) are of O(√n) complexity.
This task is uHowever, this is not viable task.
Family relations is a very simple task, yet flexible enough to almost equally support both tree option.
We should only focus on one gender, or at least ensure that persons used do not have 2 parents; the programmable tree structure does require a single parent for each node (except root).
Three tasks are to be created with the same set of relations and they differ solely on the way information is presented.
Subject is given relationship data in description provided below - depends on which group he belongs to. He is required to imagine and create a structure to hold this data in the program (discussion required: a subject can select any structure type? -> but all are strongly inferior to programmable trees even at first glance), and afterwards perform some number of subtasks with this structure (should he be given these tasks before he finishes structure creation?). Several variables are measured during this test: required time, written lines of code, mental representation of the problem (?).
The following tree main tasks are just examples, but should be considered valid.
Two formats are provided: First with just core data and the second with neat descriptive sentences. Which is better? (I lean towards the first)
| 1st task |
2nd task |
3rd task |
|
Benjamin is son from Alfred. Christopher is son from Alfred. David is son from Benjamin. Eric is son from Christopher. Frank is son from Christopher. George is son from Christopher. Hector is son from Christopher. Isaac is son from Christopher. Luke is son from Frank.
or
Alfred has 2 sons: Benjamin and Christopher. Benjamin has only one son: David. Christopher's children are named: Eric, Frank, George and Hector. Frank also has 2 sons, who are named Isaac and Luke.
|
Benjamin is son from Alfred. Christopher is brother from Benjamin. David is son from Benjamin. Eric is son from Christopher. Frank is brother from Eric. George is brother from Frank. Hector is brother from George. Isaac is son from Christopher. Luke is brother from Isaac.
or
Alfred is a parent from Benjamin. Benjamin has one brother, Christopher, and is parent to David. Christopher's eldest son is Eric. Eric has brothers: Frank, George and Hector. Frank's eldest son is Isaac and his brother is named Luke. |
Benjamin is son from Alfred. Christopher is son from Alfred. Christopher is brother from Benjamin. David is son from Benjamin. Eric is son from Christopher. Frank is brother from Eric. Frank is son from Christopher. George is brother from Frank. George is son from Christopher. Hector is brother from George. Hector is son from Christopher. Isaac is son from Christopher. Luke is brother from Isaac. Luke is son from Frank. |
| This task should spark mental model in form of the 'children direct' tree. | This task should spark mental model in form of the 'children in list' tree. | This task should not be biased towards any tree. |
Afterwards the subject is required to write additional short functions, that will:
Unfortunately, it seems that even this task is slightly biased (towards less available - 'children in list' tree implementation).
But this is less significant bias...